백트래킹 이란?
백트래킹은 알고리즘 기법 중 하나로, 재귀적으로 문제를 하나씩 풀어나가되 현재 재귀를 통해 확인 중인 상태(노드)가 제한 조건에 위배되는지(유망하지 않은지) 판단하고 그러한 경우 해당 상태(노드)를 제외하고 다음 단계로 나아가는 방식이다.
여기서 알아둘 것은 특정 상태(노드)를 제외한다는 것이다.
백트래킹은 현재 상태(노드)에서 다음 상태(노드)로 나아갈 수 있는 모든 경우를 찾되, 그 중 유망하지 않다면 현재에서 더 이상 나아가지 않고 이전의 상태(노드)로 돌아가 다음 상태(노드)를 검사한다.
여기서 더 이상 탐색할 필요가 없는(유망하지 않은) 상태(노드)를 제외하는 것을 가지치기(pruning)라고도 한다.
즉, 이 방법을 통해 우리는 모든 경우의 수를 체크 하지 않고 필요한 것만 체크하여 전체 풀이 시간을 단축할 수 있게 된다!
백트래킹을 사용하는 알고리즘 중 하나는 대표적으로 DFS가 있다. (관련 포스팅은 여기) DFS는 재귀를 통해 가능한 경로 중 유망한 경로만 찾아서 탐색을 수행한 뒤 다시 돌아와 그 중 가장 최적의 경로를 반환한다.
백트래킹을 사용해 해결할 수 있는 문제는 의사 결정, 최적화, 열거하기 등의 경우가 있다.
사실 백트래킹은 사용 가능한 경우가 많지만 시간복잡도가 보통 Exponential(지수, 2n 꼴)이며, 대부분 Dynamic Programming, 그리디 알고리즘 등으로 더 빠르게 해결할 수 있다.
하지만 일부 경우의 문제들은 여전히 백트래킹으로만 해결이 가능한 문제도 있으며 그러한 경우에 많이 사용된다.
백트래킹 실행 순서


백트래킹은 DFS(깊이 우선 탐색)을 먼저 실행하면서 더 이상 탐색을 진행할 수 없는 상황이면 다시 되돌아 가서(백트래킹) 탐색을 진행한다.
N과 M (1) 풀어보기
자연수 N이 주어지면 1부터 N까지 자연수 중에서 중복 없이 M개를 고른 수열을 출력하면 된다.
예를 들어,
N : 3 , M : 3 일때, 중복 없이 아래 처럼 출력시키면 된다.
------------------------------------------------
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1
일단 for문을 돌면서
for(int i=1; i<=N; i++) {
arr[index] = i; // i를 배열에 넣는다.
visited[i] = true; // i를 방문했다고 체크
recursion(index + 1); // 다음 인덱스 원소를 넣기 위해 (index+1)재귀 호출을 한다.
visited[i] = false; // 위에 recursion이 끝났으므로, 다음 i로 넘어가기 전에 현재 i의 방문여부를 false로 바꿔준다.
}
- 1-1) i = 1 일 때

1을 방문했다고 표시한 뒤, 다음 1을 방문할 때 -> 이미 방문 했으므로 건너 뛰게 된다. (해당 i의 visited 값 확인)
// visited [O,X,X]
for(int i=1; i<=N; i++) {
if(!visited[i]) {
// 방문 여부 확인! (안했을 경우에만 실행)
visited[i] = true; // 방문 안했으면 해당 i의 visited 값을 true로 변경!
}
}
- 1-2) 현재 i는 2이다.
그다음 2를 방문할때는 visited[2] = false 이므로 방문 한다.


또 for문으로 1,2,3을 재 방문을 하기전에, i = 1, 2 -> 이미 방문 했기 때문에 건너 뛰게 되고, 3 은 visited[3] = false 이기 때문에, 방문할 수 있다.
//visited [O,O,X]
for(int i=1; i<=N; i++) {
if(!visited[i]){
// i=3일 경우에만 해당!
visited[3] = true;
arr[index] = 3;
recursion(index + 1);
}
}
재귀 호출을 할때 넘겨주는 index값이 M과 같아 지는 시점에 출력을 하도록 한다.
// visited [O,O,O]
// arr [1,2,3]
// index = 3 , M = 3
if(index == M){ // 넘겨 받은 index가 M과 같아지는 시점에 실행
for(int i=0; i<M; i++){
System.out.print(arr[i] + " ");
}
System.out.println();
}
- 1-3) 현재 i는 3이다.

여기서 우리가 3을 방문 할 수 있는 이유는? 우리는 전에 1 -> 2-> 3 순으로 방문을 했기 때문에 visited[3]=true로 설정 되어 있을 것이다.
이전에 1->2->3을 종료 한 뒤에, 다시 visited[3]을 false로 바꿔 주어야 하고,

다시 1->2를 종료 할 때도, visited[2]를 false로 바꿔 주어야 한다.
이것을 코드로 나타 내면 ?
for(int i=1; i<=N; i++) {
arr[index] = i;
visited[i] = true;
recursion(index + 1);
// recursion이 끝나면, 자식 노드를 방문을 다했다는 의미이므로 다시 visited[i] = false로 변경
visited[i] = false; // * 이 부분!
}
그럼 다시 이전 단계로 되돌아 가면,
- 1-3) i = 3일 때

visited[3] = true로 체크 해주고, 넘겨 받은 index(2)에 i값인 3을 넣어준다.
// visited [O,X,O]
for(int i=1; i<=N; i++) {
if(!visited[i]){
visited[i] = true;
arr[index] = i;
recursion(index + 1);
visited[i] = false;
}
}그리고 다음 1,2,3 노드들을 방문을 하게 되면,
- 1-3-2) visited[1], visited[3] = true;
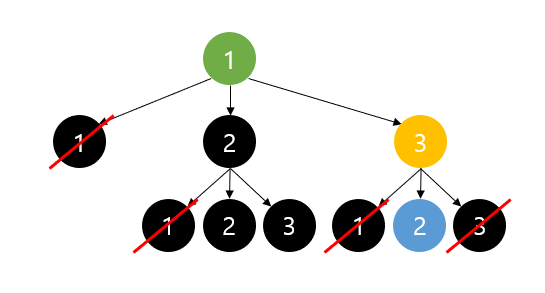
유일하게 남은 노드는 2이므로 visited[2] = true, 넘겨 받은 index에 현재 i(2)값을 넣어준다.
// visited [O,O,O]
// arr [1,3,2]
// index = 2, M = 3
for(int i=1; i<=N; i++) {
// 1, 3 건너 뜀. i=2일 때만 실행
if(!visited[2]){
visited[2] = true;
arr[index] = 2;
recursion(index + 1);
visited[2] = false;
}
}여기서 recursion(index + 1) -> recursion(3) 을 호출하게 되면,
if(index == M){ // index : 3, M : 3
for(int i=0; i<M; i++) {
System.out.print(arr[i] + " ");
}
System.out.println();
} 출력
1 3 2
이대로 계속 반복하면 된다.
전체 코드
import java.io.*;
import java.util.StringTokenizer;
public class Main {
static int N, M;
static int[] arr;
static boolean[] isUsed;
static BufferedWriter bw;
public static void main(String[] args) throws IOException {
BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
bw = new BufferedWriter(new OutputStreamWriter(System.out));
StringTokenizer st = new StringTokenizer(bf.readLine());
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
arr = new int[M+1];
isUsed = new boolean[N+1];
recursion(0);
bw.flush();
bw.close();
}
private static void recursion(int K) throws IOException {
if (K == M) { // 모든 배열의 원소가 찼을 때,
for (int i = 0; i < M; i++) {
bw.write(arr[i] + " ");
// 만약 여기서 배열의 들어있는 값의 방문여부를 false로 해주는건? -> 그러면 다시 돌아갔을 때, 중복이 나오게 된다.
// ex) isUsed[arr[i]] = false; ? 어떻게 될까?? X
}
bw.write("\n");
return ;
}
for (int i = 1; i <= N; i++) { // [1, ] [2, ] [3, ] 이런식으로 호출하게끔
if (!isUsed[i]) { // 사용 안했을 때만, 실행
arr[K] = i; // arr[인덱스]에 i값을 넣어주고
isUsed[i] = true; // 방문 여부 표시!
recursion(K + 1); // 배열의 다음 칸을 채우기 위해서 K를 +1해주고 다시 재귀로 돌린다. K++를 해주면 안되는 이유: for문을 돌렸을때, IndexOutOfBoundExcepiton 발생 간으!
isUsed[i] = false; // recursion이 다 수행됐다면, 출력도 끝났다는 의미이니, 이제 해당 i값이 유지될때, 방문여부를 없애준다.(어차피 현재 for문은 이전 i값을 사용 안한다.)
}
}
}
}https://iseunghan.tistory.com/241
참고) DFS와 백트래킹(Backtracking)의 차이
DFS는 기본적으로 그래프 형태 자료구조에서 모든 정점을 탐색할 수 있는 알고리즘 중 하나이다. 깊이를 우선적으로 탐색하기에 재귀 또는 스택을 이용한다.
재귀를 이용하여 탐색을 수행한다는 부분에서 완전탐색 알고리즘의 재귀 / 백트래킹(Backtracking)과 유사한 측면이 보여 혼란이 올 수 있다.
그런데, 재귀라는 것은 말 그대로 스스로의 함수(또는 메소드)를 호출하는 방식을 의미하는 것이므로 DFS가 재귀라는 방식을 이용해 탐색을 수행하는 것으로 하나의 방식이라고 이해하면 된다.
또한 백트래킹(Backtracking)은 재귀를 통해 알고리즘을 풀어 가는 기법 중 하나로 가지치기(Pruning)을 통해서 탐색을 시도하다가 유망하지 않으면 추가 탐색을 하지 않고 다른 해를 찾는 방법이다.
DFS는 기본적으로 모든 노드를 탐색하는 것이 목적이지만 상황에 따라서 백트래킹 기법을 혼용하여 불 필요한 탐색을 그만두는 것이 가능하다.
즉, DFS와 백트래킹은 유사한 부분이 있으며 기본적으로 사용 목적이 다르지만 두 기법을 혼용하여 사용하는 것이 가능하다. 완전히 다른 개념이 아니라 재귀 호출을 통한 기법 중 하나 이기 때문이다.
'Algorithm' 카테고리의 다른 글
| [Algorithm] 벨만포드(BellmanFord) 알고리즘 JAVA (0) | 2021.06.07 |
|---|---|
| [Algorithm] Hash란? (1) | 2021.06.01 |
| [Algorithm] LinkedList (0) | 2021.05.11 |
| [Algorithm] JAVA 비트 연산 (0) | 2021.04.17 |
| [Algorithm] 프로그래머스 스택/큐 프린터 in Java (0) | 2021.04.09 |

